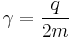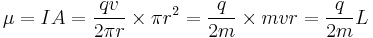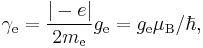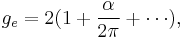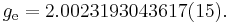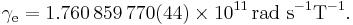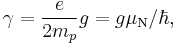Gyromagnetic ratio

In physics, the gyromagnetic ratio (also sometimes known as the magnetogyric ratio in other disciplines) of a particle or system is the ratio of its magnetic dipole moment to its angular momentum, and it is often denoted by the symbol γ, gamma. Its SI units are radian per second per tesla (s⁻¹·T ^-1) or, equivalently, coulomb per kilogram (C·kg⁻¹).

The term "gyromagnetic ratio" is sometimes used^[1] as a synonym for a different but closely related quantity, the g-factor. The g-factor, unlike the gyromagnetic ratio, is dimensionless. For more on the g-factor, see below, or see the article g-factor.

1 Gyromagnetic ratio and Larmor precession
2 Gyromagnetic ratio for a classical rotating body
3 Gyromagnetic ratio for an isolated electron
4 Gyromagnetic factor as a consequence of relativity
5 Gyromagnetic ratio for a nucleus
6 See also
7 References
- 7.1 Note 1 note
- 7.2 General note

Gyromagnetic ratio and Larmor precession

Main article: Larmor precession

Any free system with a constant gyromagnetic ratio, such as a rigid system of charges, a nucleus, or an electron, when placed in an external magnetic field B (measured in teslas) that is not aligned with its magnetic moment, will precess at a frequency f (measured in hertz), that is proportional to the external field:

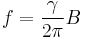$f=\frac{\gamma}{2\pi}B$ .

For this reason, values of γ/(2π), in units of hertz per tesla (Hz/T), are often quoted instead of γ.

This relationship also explains an apparent contradiction between the two equivalent terms, gyromagnetic ratio versus magnetogyric ratio: whereas it is a ratio of a magnetic property (i.e. dipole moment) to a gyric (rotational, from Greek: γύρος, "turn") property (i.e. angular momentum), it is also, at the same time, a ratio between the angular precession frequency (another gyric property) ω = 2πf and the magnetic field.

Gyromagnetic ratio for a classical rotating body

Consider a charged body rotating about an axis of symmetry. According to the laws of classical physics, it has both a magnetic dipole moment and an angular momentum due to its rotation. It can be shown that as long as its charge and mass are distributed identically (e.g., both distributed uniformly), its gyromagnetic ratio is

$\gamma = \frac{q}{2m}$

where q is its charge and m is its mass. The derivation of this relation is as follows:

It suffices to demonstrate this for an infinitesimally narrow circular ring within the body, as the general result follows from an integration. Suppose the ring has radius r, area A = πr², mass m, charge q, and angular momentum L=mvr. Then the magnitude of the magnetic dipole moment is

$\mu = IA = \frac{qv}{2\pi r}\times\pi r^2 = \frac{q}{2m}\times mvr = \frac {q}{2m} L$

as desired.

Gyromagnetic ratio for an isolated electron

An isolated electron has an angular momentum and a magnetic moment resulting from its spin. While an electron's spin is sometimes visualized as a literal rotation about an axis, it is in fact a fundamentally different, quantum-mechanical phenomenon^[2] with no true analogue in classical physics. Consequently, there is no reason to expect the above classical relation to hold. In fact it does not, giving the wrong result by a dimensionless factor called the electron g-factor, denoted g_e (or just g when there is no risk of confusion):

$\gamma_\mathrm{e} = \frac{|-e|}{2m_\mathrm{e}}g_\mathrm{e} = g_\mathrm{e} \mu_\mathrm{B}/\hbar,$

where μ_B is the Bohr magneton. As mentioned above, in classical physics one would expect the g-factor to be 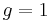$g=1$ . However in the framework of relativistic quantum mechanics,

$g_e = 2(1%2B\frac{\alpha}{2\pi}%2B\cdots),$

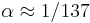where $\alpha\approx 1/137$ is the fine-structure constant. Here the small corrections to the relativistic result 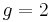$g=2$ come from the quantum field theory. Experimentally, the electron g-factor has been measured to twelve decimal places:^[3]

$~g_\mathrm{e} = 2.0023193043617(15).$

The electron gyromagnetic ratio is given by NIST^[4] as

$\gamma_\mathrm{e} = 1.760\,859\,770(44) \times 10^{11}\, \mathrm{rad\ s^{-1}T^{-1}}.$

The g-factor and γ are in excellent agreement with theory; see Precision tests of QED for details.

Gyromagnetic factor as a consequence of relativity

Since a gyromagnetic factor equal to 2 follows from the Dirac's equation it is a frequent misconception to think that a g-factor 2 is a consequence of relativity; it is not. The factor 2 can be obtained from the linearization of both the Schrödinger equation and the relativistic Klein-Gordon equation (which leads to Dirac's). In both cases a 4-spinor is obtained and for both linearizations the g-factor is found to be equal to 2; Therefore, the factor 2 is a consequence of the wave equation dependency on the first (and not the second) derivatives with respect to space and time.^[5]

Gyromagnetic ratio for a nucleus

Protons, neutrons, and many nuclei carry nuclear spin, which gives rise to a gyromagnetic ratio as above. The ratio is conventionally written in terms of the proton mass and charge, even for neutrons and for other nuclei, for the sake of simplicity and consistency. The formula is:

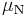$\gamma = \frac{e}{2m_p}g = g \mu_\mathrm{N}/\hbar,$

where $\mu_\mathrm{N}$ is the nuclear magneton, and g is the g-factor of the nucleon or nucleus in question.

The gyromagnetic ratio of a nucleus is particularly important because of the role it plays in Nuclear Magnetic Resonance (NMR) and Magnetic Resonance Imaging (MRI). These procedures rely on the fact that nuclear spins precess in a magnetic field at a rate called the Larmor frequency, which is simply the product of the gyromagnetic ratio with the magnetic field strength.

Approximate values for some common nuclei are given in the Table below.^[6] ^[7]

Nucleus	γ / 10⁶ rad s⁻¹ T⁻¹	γ/2π / MHz T⁻¹
¹H	267.513	42.576
²H	41.065	6.536
³He	-203.789	-32.434
⁷Li	103.962	16.546
¹³C	67.262	10.705
¹⁴N	19.331	3.077
¹⁵N	-27.116	-4.316
¹⁷O	-36.264	-5.772
¹⁹F	251.662	40.053
²³Na	70.761	11.262
³¹P	108.291	17.235
¹²⁹Xe	-73.997	-11.777

References

Note 1 note

^Note 1 : Marc Knecht, The Anomalous Magnetic Moments of the Electron and the Muon, Poincaré Seminar (Paris, Oct. 12, 2002), published in : Duplantier, Bertrand; Rivasseau, Vincent (Eds.) ; Poincaré Seminar 2002, Progress in Mathematical Physics 30, Birkhäuser (2003), ISBN 3-7643-0579-7.

General note

^ For example, see: D.C. Giancoli, Physics for Scientists and Engineers, 3rd ed., page 1017. Or see: P.A. Tipler and R.A. Llewellyn, Modern Physics, 4th ed., page 309.
^ S J Brodsky, V A Franke, J R Hiller, G McCartor, S A Paston and E V Prokhvatilov (2004). "A nonperturbative calculation of the electron's magnetic moment". Nuclear Physics B 703 (1–2): 333–362. arXiv:hep-ph/0406325. Bibcode 2004NuPhB.703..333B. doi:10.1016/j.nuclphysb.2004.10.027.
^ B Odom, D Hanneke, B D'Urso and G Gabrielse (2006). "New measurement of the electron magnetic moment using a one-electron quantum cyclotron". Physical Review Letters 97 (3): 030801. Bibcode 2006PhRvL..97c0801O. doi:10.1103/PhysRevLett.97.030801. PMID 16907490.
^ NIST. Note that NIST puts a positive sign on the quantity; however, to be consistent with the formulas in this article, a negative sign is put on γ here. Indeed, many references say that γ<0 for an electron; for example, Weil and Bolton, Electron Paramagnetic Resonance (Wiley 2007), page 578
^ Walter Greiner Quantum Mechanics: An Introduction, Springer Verlag
^ M A Bernstein, K F King and X J Zhou (2004). Handbook of MRI Pulse Sequences. San Diego: Elsevier Academic Press. p. 960. ISBN 0-1209-2861-2.
^ R C Weast, M J Astle, ed (1982). Handbook of Chemistry and Physics. Boca Raton: CRC Press. p. E66. ISBN 0-8493-0463-6.